動的計画法は、最適化のために広く使用され、頻繁に使用される概念です。この記事では、競争力のあるコーディングとほとんどすべてのコーディング面接で最もよく知られている概念の 1 つである動的計画法の概念を紹介します。
動的プログラミング入門
動的計画法とは、複雑な問題を再帰的に単純なサブ問題に分解することによって単純化することを指し、通常はボトムアップ アプローチです。
また、機械学習のフル コースを無料でお読みください。
動的計画法を適用するには、問題に「最適部分構造」と「重畳部分問題」という 2 つの重要な属性が必要です。その最適化を達成するために、動的プログラミングは暗記と呼ばれる概念を使用します。
動的計画法の応用
動的プログラミングの基本的な考え方は、複雑な問題をいくつかの小さくて単純な問題に分解し、それらを繰り返すことです。繰り返し計算される単純な部分問題を特定できる場合、その問題に対する動的計画法のアプローチがある可能性があります。
このセクションのタイトルは「動的プログラミングのアプリケーション」であるため、動的プログラミング アルゴリズムを構築するプロセスよりもアプリケーションに焦点を当てます。
フィボナッチ数:
フィボナッチ数は、従来の再帰的アプローチが多くの繰り返し計算を行うため、動的計画法のホット トピックです。これらの例では、f (0) =f (1) =1 の基本ケースを使用します。
フィボナッチ (4) の再帰ツリーの例を次に示します。繰り返しの計算に注意してください:
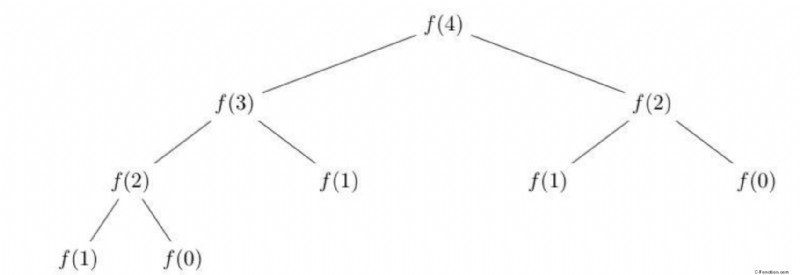
非動的プログラミング 0(2 ^ n) 実行の複雑さ、0(n) スタックの複雑さ:
これは、問題を記述する最も直感的な方法です。フィボナッチ呼び出し (n-1) を行う最初の再帰的分岐を下り、ベース ケース n <2 に到達するまで、スタック スペースはせいぜい 0(n) です。
保存された 0(n) の実行の複雑さ、0(n) のスペースの複雑さ、0(n) のスタックの複雑さ:
ストアド アプローチでは、以前のすべての関数呼び出しと同様に見なすことができる配列を導入します。位置メモ [n] は、フィボナッチ関数呼び出し (n) の結果です。これにより、重複する関数呼び出しを計算する必要がなくなるため、0 (n) の空間複雑度を 0 (n) ランタイムに交換できます。
反復動的プログラミング O (n) 実行の複雑さ、O (n) 空間の複雑さ、再帰スタックなし:
問題を基本的な部分に分解すると、フィボナッチ (n) を計算するには、フィボナッチ (n-1) とフィボナッチ (n-2) が必要であることがわかります。さらに、上記のように、基本ケースがこの再帰ツリーの最後に表示されることがわかります。
この情報を使用して、基本ケースから始めて上向きに作業して、逆に解を計算することが理にかなっています。さて、フィボナッチ (n) を計算するには、まず n までのすべてのフィボナッチ数を計算します。
ここでの主な利点は、0 (n) ランタイムを維持しながら再帰スタックを排除したことです。残念ながら、スペースの複雑さはまだ 0 (n) ですが、これも変更できます。
高度な反復動的プログラミング 0 (n) 実行の複雑さ、0 (1) 空間の複雑さ、再帰スタックなし:
前述のように、反復プログラミング アプローチは基本ケースから開始し、最終結果まで機能します。
空間的複雑度 0 (1) (定数) に到達するための重要な観察は、再帰スタックに対して行ったのと同じ観察です。フィボナッチ ( n)。これは、繰り返しのどの時点でも、フィボナッチ (n-1) とフィボナッチ (n-2) の結果を記録するだけでよいことを意味します。
これらの最後の 2 つの結果を格納するには、サイズ 2 の配列を使用し、i% 2 を使用して割り当てたインデックスを返します。これは、0、1、0、1、0、1、.. .、i% 2 のように交互になります。
加算が可換であることがわかっているため、配列の 2 つのインデックスを加算します (5 + 6 =11 および 6 + 5 ==11)。結果は、2 つのスポットのうち最も古いものに起因します (i% 2 と記されています)。最終結果は n% 2 の位置に保存されます。
後続の関数呼び出しへの応答のキャッシュを構築し、場合によっては 0 回の呼び出しを行うため、大規模な計算を何度も行う関数については、反復的で記憶されたソリューションを考え出す方が良い場合があることに注意することが重要です。 (1)は計算済みです。これが動的計画法です。
動的計画法の概念に関するこの記事が気に入っていただければ幸いです。以下のコメント欄で貴重な質問をお気軽にどうぞ。