要素のコレクションを並べ替えるには、ある要素が他の要素よりも小さい場合を判断する並べ替え述語を提供する必要があります。この述語は、cppreference.Wait に従って、「等価クラスで厳密な合計順序付けを誘導する」必要があります。 P>
今後の C++ 宇宙船オペレーターは、3 者間比較を実装します。 < の結果を返すことができる単一の関数です 、 == と > しかし、これに関連する「強い等式」や「弱い順序付け」などの用語は、数学の知識がないと多少混乱します。
このシリーズでは、等号と順序付けの背後にある数学について説明し、比較演算子と宇宙船演算子を実装するための具体的なガイドラインを示します。
このパートでは、順序付け関係の背後にある数学について説明します。順序関係は、これまで見てきた同値関係よりもはるかに複雑です。私のブログの投稿はとにかく長いので、2 つに分割することにしました。次の部分 (既に公開されています) は、C++ でどのように実装する必要があるかについてです。
要素間の順序付け
任意の 2 つの要素 a,b を検討してください セット A から .次のいずれかの関係を持つことができます:
aそしてb等しいことができます (つまり、a = b)ab未満にすることができますabよりも大きくなる可能性がありますabに相当します (つまり、大きくも小さくもなく、等しくもありません)aとb比類のないものである (つまり、それよりも大きくも等しくも同等でもない)
そのため、理想的な比較関係は a 間の関係全体を返すことができます。 と b 一度に.しかし、シリーズの最初の部分を覚えている場合、バイナリ関係は、関係にあるすべてのペアをリストすることによって定義されます.つまり、ペアが関係にあるか、またはそうではありません。
したがって、順序関係は、これらの質問の 1 つだけに答える二項関係の観点から定義されます。他の質問は、その答えに基づいて推定されます。
二項関係の候補は「a」 b 未満 」、「a b 以下 」、「a b より大きい 」および「a」 b 以上 残念ながら、2 つの異なる理論が展開されました。1 つは「a」に基づくものです。 b 未満 」と「a」に基づくもの b 以下
これは混乱を招く可能性があるため、それらを見るときは十分に注意してください。
≤ 注文関係:予約注文
「以下」の最も基本的な順序関係は予約注文です。これは (very ) 一般化された ≤ .
≤ の基本的な特性は何ですか? ?
- すべての要素はそれ自体以下であるため、再帰的です (
a ≤ aすべてのaに当てはまります ). a ≤ bの場合 とb ≤ c、さらにa ≤ c、つまり推移的です。
予約注文にはこれら 2 つのプロパティしかありません。つまり、注文とは言えません。
例として、有向グラフを考えてみましょう。ノード B と言います。 A から到達可能です A から始まるパスがある場合 最終的に B につながる .If B A から到達可能です 、 A ↦ B と書きます .
この ↦ 関係は事前注文です:すべてのノードはそれ自体から到達可能です (A ↦ A ) 単純にその場にとどまることで、反射的になります。さらに、A ↦ B の場合 と B ↦ C 次に、両方のパスを連結して A からのパスを取得できます C へ 、だから A ↦ C つまり、推移的でもあります。
ただし、接続されていないグラフがある場合は、2 つのノード A を持つことができることに注意してください。 および B どこでも A ↦ B B ↦ A でもありません A から先に進む方法がないため B まで どちらの方向にも!
したがって、予約注文がある場合、すべての要素を他のすべての要素と比較できるという保証はありません。比類のない要素が存在します。比類のない要素が必要ない場合は、完全な関係が必要です。二項関係 R 要素のペアごとに a の場合、合計です および b 、 a R b または b R a 、または両方。
そのため、事前注文の合計は、比類のない要素のないバイナリ関係です:a のいずれか b 以下です または b a 以下です (または両方!)↦ 他のすべてのノードからすべてのノードに到達できるグラフの合計です。
a ≤ b と a ≤ b の両方が そして ≤ 任意のプレオーダー ≤ の場合 ?
さて、「伝統的な」 ≤ で これは、要素が等しいことを意味します。おそらく、このより「一般的な」~ それはそれらが同等であることを意味しますか?
実際、それらは:等価関係を定義できます (それを a ~ b と呼びましょう) ) a ≤ b と言って b ≤ a の場合のみ と a .実際に同値関係であることを確認してみましょう:
a ≤ aごとにa ~ aは本当です そして当然a ~ b(再帰)- if
a ≤ b、次にb ≤ aとb ≤ a、またa ≤ bとb ~ a、だからa ~ b(対称) - if
b ~ cとa ≤ b、次にb ≤ aとb ≤ cとc ≤ bと≤、a ≤ cの推移性によりc ≤ aも真実でなければなりません とa ~ c、意味≲(他動詞)
そのため、予約注文は < と呼ばれることがよくあります。 = ではないため または < しかし ~ または ↦ .A ↦ B で定義される同値関係 双方向で到達可能な関係にすべての要素を置きます。
最後に、無向グラフの例を考えてみましょう。今度は B ↦ A ≲ を意味します パスを逆にたどることができるからです.これは、私たちの前順序が対称であることを意味します.しかし、再帰的、推移的、および対称的である二項関係は同値関係です!したがって、同値関係は特殊な前順序です.
要約すると、予約注文 a ≲ b が与えられた場合 、2 つの要素は次のいずれかになります:
- 未満 (例:
b ≲ ab ≲ aではありません ) - より大きい (例:
a ≲ ba ≲ bではありません ) - 同等 (例:
b ≲ aとa ≲ b) - 比類のない (どちらも
b ≲ a≤でもありません )、合計ではない予約注文のみ。
予約注文を使用して同等かどうかを確認する方法はないことに注意してください。
R 注文関係:部分注文と全体注文
何らかの同等性ではなく真の同等性を得られる順序関係が必要な場合はどうすればよいでしょうか?
次に、反対称性が必要です:二項関係 a R b b R a の場合、反対称です と a = b 両方とも true で、≤ も (逆も然り)
反対称の前順序がある場合、部分順序があります。つまり、再帰的、推移的、反対称のバイナリ関係です。これで、シンボル ↦ を真に使用できます。 それは実際には「より小さいか等しい」という意味だからです
「到達可能」関係 A ↦ B は予約注文でしたが、部分的な注文ではありません:B ↦ A を持つことができます と A ≠ B A の場合 (同じサイクルの一部である必要があるだけです)。
半順序の標準的な例は、セットに関連しています。セットには要素が含まれているだけですが、同じ要素が複数のセットに含まれる場合があります。セット B がある場合 いくつかの要素とセット A を含む 同じ要素 (さらにいくつかの要素) を含む場合、B と言います。 A のサブセットです (B のすべての要素 A ⊆ B の要素でもあります )、A = {1, 2, 3, 4} と表記 .
たとえば、B = {0, 1, 2, 3, 4, 5} とします。 と A ⊆ B .その後 C = {2, 3, 4, 5} .ただし、A ⊆ C の場合 A は正しくありません なぜなら 1 C を含む しかし A
部分集合の関係は明らかに事前順序ですが、半順序でもあります:B のすべての要素の場合 A ⊆ B の要素です (B ) および A のすべての要素 B ⊆ A の要素です (A )、B と A = B 同じ要素が含まれている必要があります.So ⊆ 意味 A = {1, 2} 非対称です。
名前が示すように、半順序はまあ、部分的です。 、つまり合計ではありません。 B = {3, 4, 5} を考慮してください と A .B と A ⊆ B まったく異なる要素が含まれているため、どちらの B ⊆ A も含まれていません ≤ でもありません
比類のない要素のない部分順序がある場合、それは全体順序と呼ばれます。これは、再帰的、推移的、反対称的、全体的なバイナリ関係です。
彼らは ≤ です ≤ のように直感的に 数の関係。
要約すると、部分順序 a ≤ b が与えられた場合 、2 つの要素は次のいずれかになります:
- 未満 (例:
b ≤ ab ≤ aではありません ) - より大きい (例:
a ≤ ba ≤ bではありません ) - 等しい (例:
b ≤ aとa ≤ b) - 比類のない (どちらも
b ≤ a<でもありません )、ただし半順序のみ。
予約注文との唯一の違いは、同等ではなく同等であることに注意してください。
< 順序関係:厳密な部分順序と厳密な全体順序
a < a に関して定義された順序関係を見てみましょう a < a であるため、明らかに再帰的ではありません。 決して真実ではありません。代わりに、それらは非反射的であり、a < b と述べているだけです
事前注文で行ったのと同様の精神で始めましょう:非反射的かつ推移的な二項関係を使用します。このような二項関係は、厳密な半順序と呼ばれます。
待って、なに?
「厳密な予約注文」と呼ばれないのはなぜですか?
追加のプロパティを自動的に取得するため:推移的であるため b < c と a < c a < b を意味します .これは、b < a がある場合を意味します そして a < a 、それは a, b を意味します !これは非反射性と矛盾するので、2 つの要素はありません a < b どこで b < a と < は同時に真です。これが真である二項関係は非対称と呼ばれます。そのため、非反射的で推移的なすべての二項関係も非対称です。
≤ を拡張するとどうなるかを考えてみましょう (a, a) に注文する すべての a ≤ b を追加して セットへのペア。If b ≤ a と a = b が true の場合、非対称性は (a, a) であることを意味します .これは、非反射的かつ推移的な二項関係の拡張が半順序であることを意味します.そして、半順序から始めてA ⊆ Bをすべて削除すると 対になると、非反射的で推移的な二項関係になります。
したがって、非反射的かつ推移的な二項関係は、厳密な半順序と呼ばれます。
厳密な半順序の例として、サブセット関係 A ⊂ B を使用できます。 それを厳密なサブセット関係 B に変換します これは A の場合にのみ当てはまります A で同じ要素が含まれています a < b と等しくない 繰り返しますが、厳密な半順序は完全である必要はありません。同じセットの例が現在も有効であり、比類のない要素を示しています。
また、厳密な半順序が全順序である場合、それを厳密な全順序と呼びます。
しかし待ってください:b < a のいずれかの場合、二項関係は合計であると言いました または a すべての b に対して そして a < a .しかし、非対称性は a, b を意味します 決して真実ではないので、合計ではありません!
したがって、厳密な全順序は実際には全順序ではありません。代わりに、三分法と呼ばれるものがあります:2 つの要素ごとに a < b 、いずれか b < a または a = b または a < b (ただし、同時に真となるのはそのうちの 1 つだけです)。
b < a がない場合の厳密な半順序 < でもありません 要素が等しいか、比較できないかのいずれかです。厳密な全順序の場合、要素が等しいことを意味します。
これは、厳密な部分順序が部分順序よりも「強力ではない」ことを意味します。厳密な部分順序 a < b を考えると 、2 つの要素は次のいずれかになります:
- 未満 (例:
b < a) - より大きい (例:
a < b) - 等しいまたは 比類のない (つまり、どちらでもない
b < a<でもありません )、しかしどれかはわかりません!
厳密な全順序の場合にのみ、2 つの要素が実際に等しいと推測できます。
C := {yellow, red, green, blue, cyan, magenta} 順序関係:厳密な弱い順序
厳密な予約注文をもう一度定義してみましょう。 (どういうわけか) 等価ではなく等価を意味する厳密な順序関係。
前回の投稿の色のセットをもう一度見てみましょう:magenta < cyan < green < red < blue < yellow .次の順序で並べることにより、厳密な部分 (この場合は全体) 順序を定義できます。 .色は < と言います このリストの最初にリストされている場合、別の色よりも優先されます。
前回、色の等価関係を調べました。ここで、シアンは単なる醜い青です。これに対応する、≲ に関する予約注文の合計 書くのは簡単です:magenta ≲ green ≲ red ≲ blue ≲ yellow 同様に cyan ≲ blue と blue ≲ cyan .Now cyan と blue 同等と見なされます。
これに基づいて厳密な順序を簡単に定義できます:If a < b が false の場合、a b より大きくなければなりません b に相当 .つまり a < b b ≲ a の場合は false 、それ以外の場合は true です。これは予約注文合計の補数です。
この場合、次の厳密な順序が得られます:magenta < green < red < blue/cyan < yellow cyan < blue でもありません blue < cyan でもありません .これは非反射的で推移的であるため、厳密な半順序ですが、厳密な全順序ではなく、三分法はなく、それの弱いバージョンのみです:a < b または b < a または a と b
このような順序関係は、厳密な弱順序と呼ばれます。これは、非反射的で推移的であり、比較不可能性が推移的である二項関係です。最後のプロパティが意味することは次のとおりです。If a と b 比類のない (つまり、どちらの a < b でもない) b < a でもありません ) と b と c 比類のない場合、a と c
そして、この性質こそが、等価関係 ~ を定義することを可能にするものです。 、ここで a ~ b a の場合 と b 比類のないものです。必要なプロパティを確認しましょう:
a < aのように再帰的です<であるため、常に false です。 反射的ではありません。a < bなので対称です とb < aaの役割を簡単に交換できるように、両方とも false でなければなりません とb.- 要件により推移的です。
これには興味深い数学的な結果があります:集合 A に対する厳密な弱い順序 A/~ と呼ばれる集合に対する厳密な全順序を定義します .このセット、つまり等価クラスのセットでは、等価なすべての要素をグループ化しました (~ によると)。 ).A/~ の 2 つの要素なし は同等であるため、このセットの厳密な弱順序は厳密な全順序です。
色は C/~ です 私の cyan に基づく blue です 等価は {yellow, red, green, blue, magenta} になります (なぜなら cyan blue です ).そして、このセットでは、a < b のいずれかであるため、合計注文があります。 または b < a または a = b (これは実際には同等を意味しますが、セットを変更してごまかしています)。
これで、導入部からの cppreference の引用を理解できます。比較述語は、「同値クラスで厳密な全順序付けを誘導する」必要があります。同等の要素が全順序。つまり、比較述語は厳密な弱順序でなければなりません。
要約すると、厳密な弱い順序の場合、2 つの要素は次のいずれかになります。
- 未満 (例:
a < b) - より大きい (例:
b < a) - 同等 (つまり、どちらでもない
a < bb < aでもありません )
まとめ
わかりました、これはたくさんでした 用語の説明です。順序関係をまとめたグラフと、一方を他方に変換する方法を次に示します。
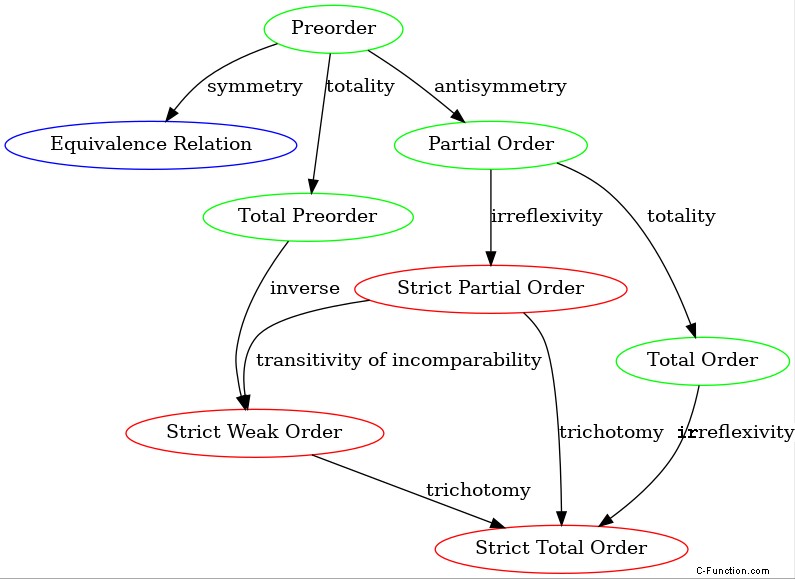
この表は、実際に何が必要かを示しています:2 つの要素 a が与えられた場合 と b およびいくつかの順序関係は a です b 未満 、より大きい、同等/等しい、または比較できない?簡潔にするために、より大きいは省略されています (単に a を入れ替えるだけです) と b ) と equal と equal はマージされます。しかし、部分順序、全順序、および厳密な全順序が真の等価を定義することはご存知でしょう。
| 順番 | 同等の場合 | 厳密にIf未満 | 比類のないIf |
|---|---|---|---|
| プレオーダー | a ≲ b と b ≲ a | a ≲ b b ≲ a ではありません | !(a ≲ b) そして !(b ≲ a) |
| 予約注文合計 | a ≲ b と b ≲ a | a ≲ b b ≲ a ではありません | 決して |
| 部分注文 | a ≤ b と b ≤ a | a ≤ b b ≤ a ではありません | !(a ≤ b) と !(b ≤ a) |
| 合計注文 | a ≤ b と b ≤ a | a ≤ b b ≤ a ではありません | 決して |
| 厳密で弱い秩序 | !(a < b) と !(b < a) | a < b | 決して |
| 厳密な部分順序 | わからない | a < b | !(a < b) と !(b < a) |
| Strict Total Order | !(a < b) と !(b < a) | a < b | 決して |
厳密な半順序は、2 つの要素が等しいか、単に比較できないかを知ることができないため、まったく役に立たないことに注意してください。また、2 つの次元に基づいて順序関係をさらに単純化できます。
- 順序は部分的ですか、それとも全体的ですか (つまり、比類のない要素ですか)?
- 順序は同等または同等を定義しますか?
| 一部 | 合計 | |
|---|---|---|
| 同等 | プレオーダー | 完全な予約注文、厳密な弱い注文 |
| 平等 | 部分注文 | Total Order、Strict Total Order |
合計列に 2 つのオプションがあるのはなぜですか?
< の間の質問です そして ≤ 関係、どちらも同様に優れています。そして、並べ替えと検索に関する将来の部分からの簡単なスポイラー:クイックソート、全順序が必要なシーケンスですが、同等性で十分です。したがって、好みに応じて、全プレオーダーまたは厳密な弱い順序のいずれかを渡すことができます。等価 < 、つまり、厳密に弱い注文です。しかし、完全な事前注文を使用することもできます。その場合、デフォルトは std::less ではありません。 しかし std::less_equal .